SEB Section 2 BFS & DFS

BFS

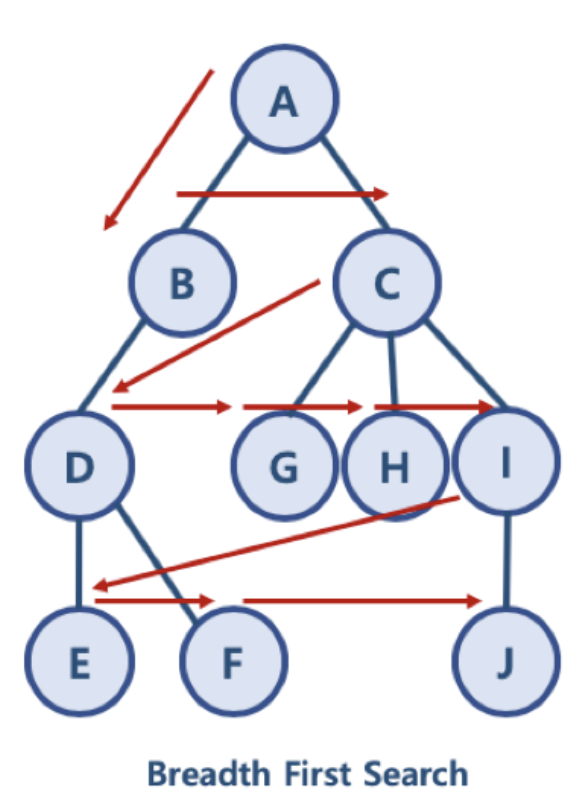
루트노드를 기준으로 가장 가까운 정점부터 탐색을 한다. 그리고 더는 탐색할 정점이 없을 때, 그다음 떨어져 있는 정점을 순서대로 방문한다. 이렇게 너비를 우선적으로 탐색하는 방법을 너비 우선 탐색이라 부른다. 최악의 경우에는 모든 경로를 다 살펴봐야 한다.

• 두개의 큐를 사용한다.
• root와 가까운 node들부터 찾기 때문에 최단거리를 탐색할 때 유용하다.
• queue에 각 노드의 정보를 기록해야 하기 때문에 메모리를 많이 잡아 먹는다.
• 찾고자 하는 target node가 root node와 가까이 있다고 예상될 경우 BFS를 사용한다.

• 지도 어플에서 특정 위치까지의 최단거리 안내, 혹은 소셜미디어에서 친구 추천등에 이용된다.

• 그래프 구현

const graph = {
  A: ["B", "C"],
  B: ["A", "D"],
  C: ["A", "G", "H", "I"],
  D: ["B", "E", "F"],
  E: ["D"],
  F: ["D"],
  G: ["C"],
  H: ["C"],
  I: ["C", "J"],
  J: ["I"],
};

• 알고리즘 구현

두 개의 큐를 활용한다.

const graph = {
  A: ["B", "C"],
  B: ["A", "D"],
  C: ["A", "G", "H", "I"],
  D: ["B", "E", "F"],
  E: ["D"],
  F: ["D"],
  G: ["C"],
  H: ["C"],
  I: ["C", "J"],
  J: ["I"],
};

const bfs = (graph, startNode) => {
  let visited = []; // 탐색을 마친 노드들
  let needVisit = []; // 탐색해야할 노드들

  needVisit.push(startNode); // 노드 탐색 시작

  while (needVisit.length !== 0) {
    // 탐색해야할 노드가 남아있다면
    const node = needVisit.shift(); // queue이기 때문에 선입선출, shift()를 사용한다.
    if (!visited.includes(node)) {
      // 해당 노드가 탐색된 적 없다면
      visited.push(node);
      needVisit = [...needVisit, ...graph[node]];
    }
  }
  return visited;
};

console.log(bfs(graph, "A"));

DFS

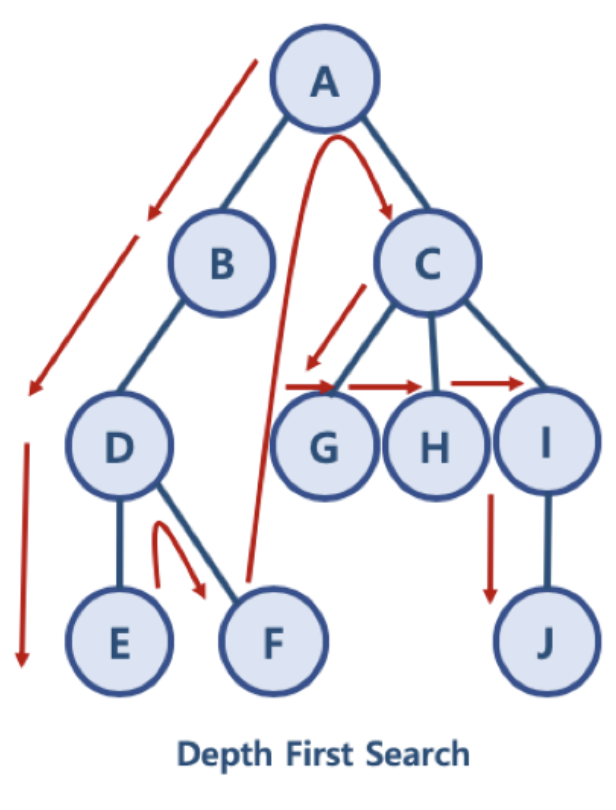
하나의 경로를 끝까지 탐색한 후, 검색 대상이 아니라면 다음 경로로 넘어가서 탐색한다. 깊이를 우선적으로 탐색 하는 것을 깊이 우선 탐색이라 부른다. 해당 경로를 완벽하게 탐색할 때 사용한다. BFS보다 탐색 시간은 조금 오래 걸려도 모든 노드를 완전히 탐색할 수 있다.

• 한 개의 큐와 한 개의 스택을 사용한다.
• BFS보다 속도가 느릴 수 있다.
• 미로 게임 등에서 경로가 존재하는지를 판별할 때 유용하다.

DFS는 이전 노드가 아니라 자기 자신과 연결되었던 노드들을 먼저 탐색하기 때문에 stack을 사용한다.

• 알고리즘 구현

const dfs = (graph, startNode) => {
  let needVisitStack = []; // 탐색을 해야 할 노드들
  let visitedQueue = []; // 탐색을 마친 노드들

  needVisitStack.push(startNode);

  // 탐색을 해야 할 노드가 남아 있다면
  while (needVisitStack.length !== 0) {
    const node = needVisitStack.pop();
    if (!visitedQueue.includes(node)) {
      visitedQueue.push(node);
      needVisitStack = [...needVisitStack, ...graph[node]];
    }
  }

  return visitedQueue;
};

console.log(dfs(graph, "A"));

시간 복잡도

DFS와 BFS 모두 노드 수 + 간선 수 만큼의 복잡도를 지닌다. 따라서 O(n)이다.